The Blackbody Background Noise

The noise limit in a SMM/THz system originates in the fluctuation in the number of photons in the thermal background [1]. Because the photons within each mode are governed by Bose-Einstein statistics, the fluctuations are given by

\begin{equation} \Delta n_m^2 = n_m\left(n_m+1\right) \end{equation}

In the long wavelength limit $n_m >> 1$ and

\begin{equation} \Delta n_\text{rms} ~ n_m. \end{equation}

For broadband detectors and in the long wavelength limit, it can be shown that the fundamental limit is [Putley, 1964 #1685;De Lucia, 2004 #14152] [2]

\begin{equation} P_N ~ kT \sqrt{B\nu_\text{max}} = kT\nu_\text{max}\sqrt{\frac{B}{\nu_\text{max}}} \label{eq:11} \end{equation}

where $\nu_\text{max}$ is the maximum optical frequency response of the detector and $B$ is the bandwidth of the integrating amplifier. The noise equivalent power is defined by normalizing this to $B$ = 1 Hz,

\begin{equation} NEP \equiv kT\sqrt{\nu_\text{max}} \label{eq:12} \end{equation}

With $\nu_\text{max}$ = 1 THz, $B$ = 1 Hz, and $T$ = 300 K, $P_N$ = 4.14 x 10^-15 W/Hz^1/2.

In contrast, heterodyne detectors can sample a small bandwidth $\Delta\nu$ at any point in the long wavelength tail of the blackbody distribution and the noise power in this bandwidth is

\begin{equation} P_N = kT\Delta\nu \end{equation}

With 300 K and $\Delta\nu$ = 1 Hz, $P_N$ ~ 4 x 10-21 W. To place this on the same basis as Eq. \eqref{eq:12}, one must assume an integrating bandwidth of B = 1 Hz as well, leading to the same numerical value. However, it should be noted that whereas $\nu_\text{max}$ = 1 THz is typical of broadband detectors, $\Delta\nu$ = 1 Hz is not typical of the bandwidths of heterodyne systems. Since this bandwidth is set by the (typically adjustable) bandwidth of the intermediate frequency (IF) amplifier, we will introduce here that this bandwidth $b$ is $\Delta\nu$.

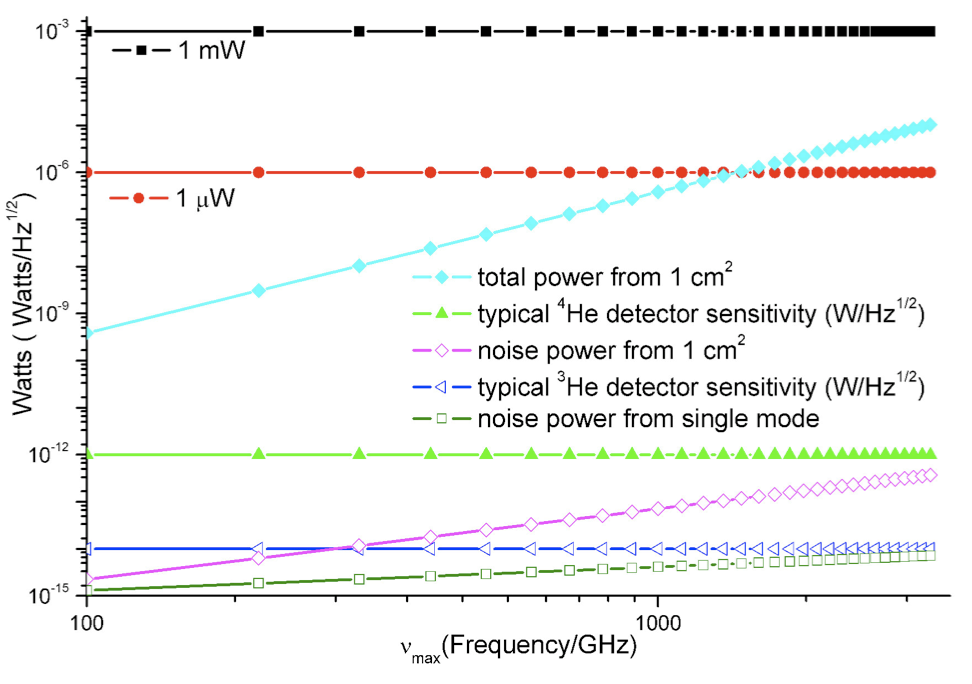
Figure: Noise and Power in the SMM Spectral Region shows noise and power as a function of the frequency cut-off $\nu_\text{max}$ with $B$ = 1 Hz for a broadband detector (for a heterodyne system it would be less). The noise power given by Eq. \eqref{eq:11} is many orders of magnitude below the thermal power. Confusion of the two (along with neglect of the single mode antenna theorem) has led to the widespread misconception that cw systems in the SMM are ‘plagued by noise’ [De Lucia, 2004 #14152]. To the contrary, it is the quiet background that has made possible so much of the activity in the SMM, even with modest power levels. Expressed another way via Eq. (8), with the bandwidth defined by a Doppler limited width of ~1 MHz, even the modest power of 1 mW corresponds to T ~ 10¹⁴ K, very bright indeed in comparison to 300 K noise.