Absorption Strengths
If the absorption coefficient of the THz power $P$ is defined by \begin{equation}\alpha = -\left(\frac{1}{P}\right)\left(\frac{\Delta P}{\Delta x}\right)\end{equation} in the microwave limit (where $h\nu << kT$), the peak absorption coefficient between two rotational levels $m$ and $n$ is \begin{equation}\alpha_{mn} = \frac{8\pi^2NF_m\nu^2}{3kTc\Delta\nu}\left|\mu_{mn}\right|^2\end{equation} where $NF_m$ is the number of molecules per unit volume in state $m$, $\nu$ is the rotational transition frequency $\Delta\nu$ the line width, and $\mu_{mn}$ is the dipole matrix element [1]. The transition moment $\mu_{mn}$ contains contributions from the components of the permanent dipole moment along each of the principal axes of the moment of inertia tensor, which determine the rotational selection rules.
Figure: Rotational Interaction Strength. Rotational interaction
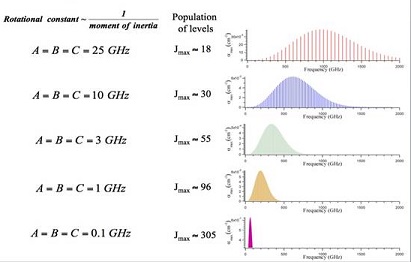
strength in the THz spectral region as a function of molecular size (i.e.
the molecular moments of inertia) and frequency.
For optimum sensitivity the gas pressure is adjusted in proportion to frequency so that the
Doppler and pressure broadening contributions to the linewidth are equal and $N/\Delta\nu$ is
independent of frequency. Because of degeneracy and rotational partition function effects, $F_m$
is often proportional to $\nu$ until declining Boltzmann population causes it to fall
exponentially. These factors typically give rise to absorption coefficients that rise as $\nu^3$
to reach a maximum at some optimum frequency in the THz before declining exponentially. This
effect can be seen in Figure: Rotational Interaction Strength
above.
References
- Microwave Molecular Spectra Techniques of Chemistry 18, 929 (John Wiley & Sons, 1984). Google Scholar